Page 35 - KP_no15full

Izotóp-hIstórIa

3. ábra

ben Ronald P.
Bell számításai
alapján. (4.
ábra)
Összetett
mechanizmusú
reakciók esetén,
amikor az egy-
mást követő
lépéseknek csak
egyike tartalmazza
az izotópos kötés felszakadását, a helyzet
bonyolultabb. Ilyen pl. az elektrofil aro-
más szubsztitúciós reakció. (5. ábra)
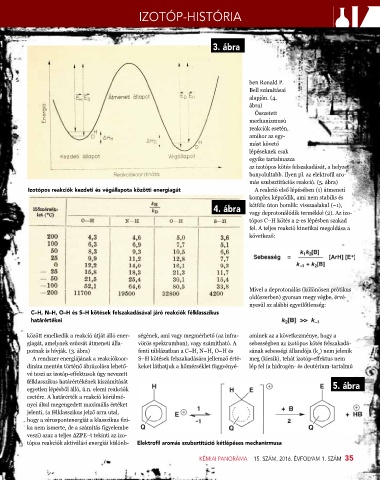
Izotópos reakciók kezdeti és végállapota közötti energiagát A reakció első lépésében (1) átmeneti
komplex képződik, ami nem stabilis és
kétféle úton bomlik: visszaalakul (–1),
4. ábra vagy deprotonálódik termékké (2). Az izo-
tópos C–H kötés a 2-es lépésben szakad
fel. A teljes reakció kinetikai megoldása a
következő:

Mivel a deprotonálás (különösen prótikus
oldószerben) gyorsan megy végbe, érvé-
nyesül az alábbi egyetlőtlenség:
C–H, N–H, O–H és S–H kötések felszakadásával járó reakciók félklasszikus
határértékei

között emelkedik a reakció útját álló ener- ségének, ami vagy megmérhető (az infra- aminek az a következménye, hogy a
giagát, amelynek csúcsát átmeneti álla- vörös spektrumban), vagy számítható. A sebességben az izotópos kötés felszakadá-
potnak is hívják. (3. ábra) fenti táblázatban a C–H, N–H, O–H és sának sebességi állandója (k ) nem jelenik
2
A rendszer energiájának a reakciókoor- S–H kötések felszakadására jellemző érté- meg (kiesik), tehát izotóp-effektus nem
dináta mentén történő ábrázolása lehető- keket láthatjuk a hőmérséklet függvényé- lép fel (a hidrogén- és deutérium-tartalmú
vé teszi az izotóp-effektusok úgy nevezett
félklasszikus határértékének kiszámítását
egyetlen lépésből álló, ú.n. elemi reakciók 5. ábra
esetére. A határérték a reakció körülmé-
nyei által megengedett maximális értéket
jelenti, (a félklasszikus jelző arra utal,
hogy a zéruspontenergiát a klasszikus fizi-
ka nem ismerte, de a számítás figyelembe
veszi) azaz a teljes ΔZPE–t tekinti az izo-
tópos reakciók aktiválási energiái különb- Elektrofil aromás szubsztitúció kétlépéses mechanizmusa

KémIaI panoráma 15. szám, 2016. évfolyam 1. szám 35